Armstrong Number in Python: Explanation & Code Examples

Learn what an Armstrong number is and how to check for it in Python. Explore different methods with examples and explanations.
An Armstrong number (also known as a narcissistic number, pluperfect digital invariant (PPDI), or narcissist number) is a number that is equal to the sum of its own digits each raised to the power of the number of digits.
What is an Armstrong Number?
A number is an Armstrong number if:
For a given n-digit number:
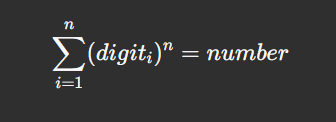
Example:
153 is an Armstrong number because:
1³ + 5³ + 3³ = 1 + 125 + 27 = 153Checking Armstrong Number in Python
We can check whether a number is an Armstrong number using different methods.
1. Using a Loop
def is_armstrong(num):
digits = [int(digit) for digit in str(num)]
power = len(digits)
total = sum(digit ** power for digit in digits)
return total == num
# Example
num = 153
print(is_armstrong(num)) # Output: True2. Using List Comprehension
def is_armstrong(num):
return num == sum(int(digit) ** len(str(num)) for digit in str(num))
# Example
print(is_armstrong(9474)) # Output: True3. Checking Armstrong Numbers in a Range
def find_armstrong_numbers(start, end):
return [num for num in range(start, end + 1) if is_armstrong(num)]
# Example: Find Armstrong numbers between 1 and 10000
print(find_armstrong_numbers(1, 10000))Armstrong Numbers Up to 10000
Some Armstrong numbers between 1 and 10000 are:
1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 9474Conclusion
Armstrong numbers are an interesting mathematical concept and checking them in Python is straightforward using loops or list comprehensions. Mastering such concepts helps in understanding number properties and improving algorithmic thinking.